Leetcode729. 我的日程安排表 I

题目链接

点我(^_^)

题意

题意就是不和之前日程重合就可以插入日程并返回true,否则返回false

解题思路

黑色代表已有日程，黄色代表待插入日程
下面代表合法的，即可插入

再看看不能插入的情况

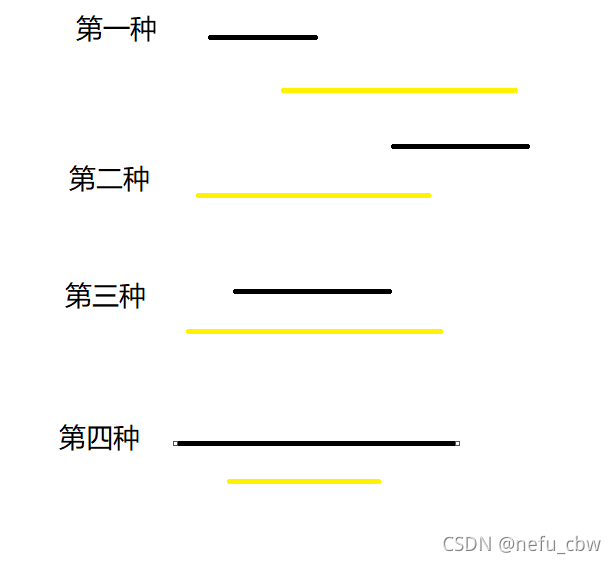
我们通过观察可以发现，所有不合法情况都是 已有日程的左端 < **待插入日程右端**，所以我们只要找已有日程中 **小于待插入日程右端** 最大的，看其右端是否 > 待插入日程左端，如果大于就不能插入，否则就能插入。
因此，我们可以维护一个有序序列，然后就可以通过二分找到 小于待插入日程右端 最大的位置。
分析一下时间复杂度，每次的二分操作是 O(logn)，插入操作是 O(n)，所以整体复杂度还是 O(n^2^)，看着和暴力法差不多，实际对于不能插入的情况，我们 O(logn) 就能判断，并且每次插入操作也不是恒定 O(n) 的，所以还是比暴力法好的。
对于平均复杂度 O(nlogn) 的算法，这里可以提供一种 权值线段树 的思路，这样每次就是恒定 O(logk) 的操作，k为日程的数字能取得大小。但是空间就不够了，可以通过动态开点解决。

具体代码

typedef pair<int,int> pii;
class MyCalendar {
public:
    vector<pii> vc;
    MyCalendar() {
        vc.clear();
    }
    
    bool book(int start, int end) {
        if(vc.empty())
        {
            vc.push_back(make_pair(start, end));
            return true; 
        }
        int l=0, r=vc.size()-1;
        int pos=0;
        while(l<=r)
        {
            int mid = (l+r)>>1;
            if(vc[mid].first >= end)
                r = mid - 1;
            else
            {
                l = mid + 1;
                pos = mid;
            }
        }
        if(vc[pos].first >= end)
        {
            vc.emplace(vc.begin(), make_pair(start, end));
            return true;
        }
        else
        {
            if(vc[pos].second > start)
                return false;
            else
            {
                vc.emplace(vc.begin()+pos+1, make_pair(start, end));
                return true;
            }
        }
    }
};