题目链接
点我(^_^)
题目大意
求矩阵中每个位置到最近0的距离(曼哈顿距离)
解题思路
思路1.BFS
bfs特性就是搜到该点了,该点就是最优解了。所以,我们可以将所有位置上为0的入队,这时队列里都是到最近0距离为0的位置,之后按bfs进行操作,即从队首取出一个元素,用它去更新其上、下、左、右四个位置,并入队。需要注意的是,之前已经被更新过的就不用再更新了,在代码部分我们用-1表示尚未被更新,并且我们可以直接在原数组上修改。这样时间复杂度为 O(n*m),空间复杂度也为 O(n*m)(最坏情况下都是0,所以都要入队)。
思路2.动态规划

这里的距离为曼哈顿距离,所以,如果一个位置被0更新,只有一下四种情况:
0在其左上方,可以通过右移x下移y到该位置0在其右上方,可以通过左移x下移y到该位置0在其左下方,可以通过右移x上移y到该位置0在其右下方,可以通过左移x上移y到该位置
所以,其实我们只要从四个角动态规划即可,例如从左上角,dp转移方程如下:
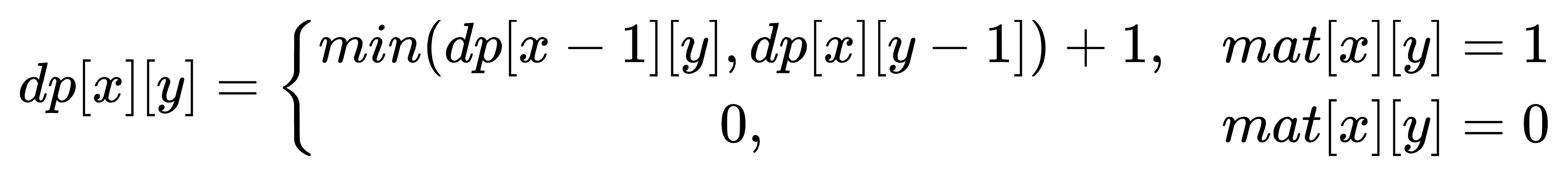
这样四次两层循环就可以解决。实际上,我们只需要两次两层循环就可以解决,例如左上角和右下角。
我们先从左上角进行dp,后从右下角进行dp,以下论证为什么这样做包含了右上角以及左下角的情况:
- 右上角
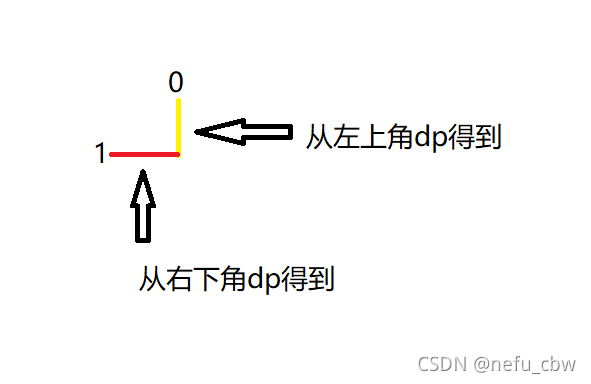
如果0在其右上角,我们在第一次dp时保存了正上方的信息,第二次dp保存了正右方的信息,这样就可以组合得到右上角0的情况。
- 左下角
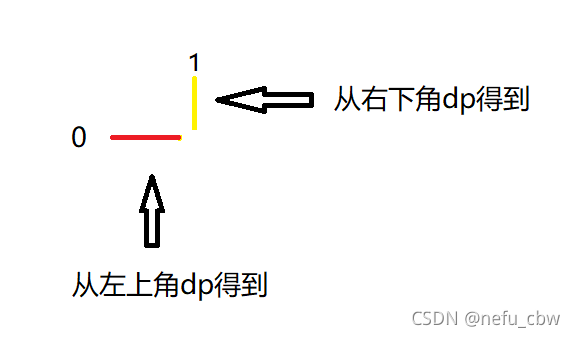
如果0在其左下角,我们在第一次dp时保存了正左方的信息,第二次dp保存了正下方的信息,这样就可以组合得到左下角0的情况。
这样的话,动态规划的时间复杂度为 O(n*m),空间复杂度为 O(1) (直接利用原数组进行操作,额外的空间就是常数空间)
具体代码
代码1.BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| typedef pair<int,int> pii;
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
int tx[4] = {0,0,1,-1};
int ty[4] = {1,-1,0,0};
queue<pii> q;
for(int i=0; i<mat.size(); ++i)
for(int j=0; j<mat[0].size(); ++j)
{
if(mat[i][j] == 0)
q.push(make_pair(i,j));
else
mat[i][j] = -1;
}
while(!q.empty())
{
pii temp = q.front();
q.pop();
for(int i=0; i<4; ++i)
{
int t_x = temp.first+tx[i];
int t_y = temp.second+ty[i];
if(t_x<0 || t_x>=mat.size() || t_y<0 || t_y>=mat[0].size() || mat[t_x][t_y]!=-1)
continue;
mat[t_x][t_y] = mat[temp.first][temp.second]+1;
q.push(make_pair(t_x,t_y));
}
}
return mat;
}
};
|
代码2.动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
for(int i=0; i<mat.size(); ++i)
for(int j=0; j<mat[0].size(); ++j)
mat[i][j] = ((mat[i][j]==1)?10000:0);
for(int i=0; i<mat.size(); ++i)
for(int j=0; j<mat[0].size(); ++j)
{
if(mat[i][j] != 0)
{
if(i-1>=0)
mat[i][j] = min(mat[i][j], mat[i-1][j]+1);
if(j-1>=0)
mat[i][j] = min(mat[i][j], mat[i][j-1]+1);
}
}
for(int i=mat.size()-1; i>=0; i--)
for(int j=mat[0].size()-1; j>=0; j--)
{
if(mat[i][j] != 0)
{
if(i+1<mat.size())
mat[i][j] = min(mat[i][j], mat[i+1][j]+1);
if(j+1<mat[0].size())
mat[i][j] = min(mat[i][j], mat[i][j+1]+1);
}
}
return mat;
}
};
|