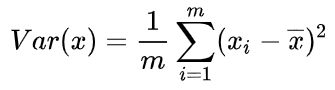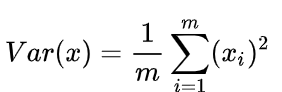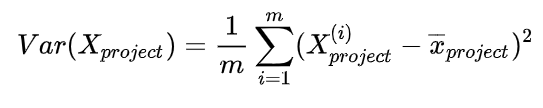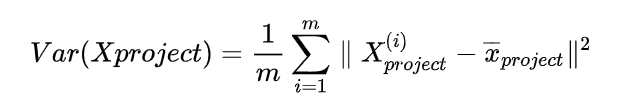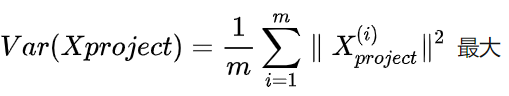引言

我们在完成一个机器学习任务比如线性回归，所使用数据的维度可能非常高(训练测试耗时大且占内存大)，或者属性之间可能具有相关性，比如奖学金和绩点（奖学金也反映了绩点的情况），这就会造成数据的冗余。这时我们就可以用到 PCA(Principal components analysis)主成分分析，来对数据进行降维，减小数据的冗余。

PCA的思想

当然，PCA 不是简单地选择几个属性或者说是去除几个属性，它是综合考虑了所有属性，确定出几个主成分（或者说是新的属性），这个主成分可以说是原始属性的综合。

所以关键就是 w1 w2 是多少。
比如下面图中，我们将样本点投影到 u1 好还是投影到 u2 好。

直观地看是 u1 比较好，为什么呢？可以有两种解释，第一种解释样本点到这个直线的距离足够近，第二种解释是样本点在这个直线上的投影能尽可能的分开。
这里我们以第二种解释来进行下面的讨论。
这里样本点在这个直线上的投影能尽可能的分开，一般我们使用方差最大来表示。

第一步，将样本进行均值归0，此时：

第二步，需要定义一个轴的方向 w=(w1,w2)，使得我们的样本，映射到 w 以后，使下面的公式最大：

其实括号中的部分是一个向量，更加准确的描述应该是：

因为前面已经去均值，所以，这里只需：

最后可以化为如下优化问题。

使用梯度上升法解决目标函数优化问题。

具体代码如下

import numpy as np
import matplotlib.pyplot as plt

X = np.empty((100, 2))
X[:, 0] = np.random.uniform(0., 100., size=100)
X[:, 1] = 0.75 * X[:, 0] + 3. + np.random.normal(0., 10., size=100) 

plt.scatter(X[:, 0], X[:, 1])
plt.show()
def demean(X):
    # 不使用standardscale标准化数据，求解PCA需要方差，只去均值。
    return X - np.mean(X, axis=0) # axis=0表示最终求得的均值是一个行向量，也就是说将每一列求和 
x_demean = demean(X)
plt.scatter(x_demean[:,0], x_demean[:,1])
plt.show()
np.mean(x_demean[:,0])
np.mean(x_demean[:,1])
def f(w ,x):
    return np.sum((x.dot(w) ** 2)) / len(x)

def df_math(w, x):
    return x.T.dot(x.dot(w)) * 2. / len(x)

def df_denug(w, x, epsilon=0.0001):
    res = np.empty(len(w))
    for i in range(len(w)):
        w_1 = w.copy()
        w_1[i] += epsilon
        w_2 = w.copy()
        w_2[i] -= epsilon
        res[i] = (f(w_1, x) - f(w_2, x)) / (2 * epsilon)
    return res

def direction(w):
    return w / np.linalg.norm(w)

def gradient_ascent(df, x, init_w, eta, n_iters=1e4, epsilon=1e-8):

    w = direction(init_w)
    cur_iter = 0
    while cur_iter < n_iters:
        gradient = df(w, x)
        last_w = w
        w = w + eta * gradient
        w = direction(w)
        if (abs(f(w, x) - f(last_w, x)) < epsilon):
            break
        cur_iter += 1
    return w

测试：

init_w = np.random.random(X.shape[1])    # 不能0向量开始
init_w
eta = 0.001
gradient_ascent(df_denug, x_demean, init_w, eta)

输出结果 array([0.7851916, 0.6192529])

w = gradient_ascent(df_math, x_demean, init_w, eta)
plt.scatter(x_demean[:, 0], x_demean[:,1])
plt.plot([0, w[0]*30], [0, w[1]*30], color='r')
plt.show()

sklearn中的PCA

我们使用 PCA 来应用在 KNN 手写数字识别任务上

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split

digits = datasets.load_digits()
x = digits.data
y = digits.target

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=666)
x_train.shape

Output：(1437, 64)

%%time
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
knn_clf.fit(x_train, y_train)

Output：Wall time: 288 ms

1	knn_clf.score(x_test, y_test)

Output：0.9888888888888889
应用 PCA

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(x_train)
x_train_reduction = pca.transform(x_train)
x_test_reduction = pca.transform(x_test)
%%time
knn_clf = KNeighborsClassifier()
knn_clf.fit(x_train_reduction, y_train)

Output：Wall time: 101 ms

1	knn_clf.score(x_test_reduction, y_test)

Output：0.6055555555555555
测试时间是下降了不少，但准确下降的也很多，这是无法接受的，可见从 64维映射到 2维，损失了很多有效的信息。

1	pca.explained_variance_ratio_

Output：array([0.1450646 , 0.13714246])
可见映射到 2 维才保留了不到 30% 的信息。

pca = PCA(n_components=x_train.shape[1])
pca.fit(x_train)
pca.explained_variance_ratio_
plt.plot([i for i in range(x_train.shape[1])],
        [np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(x_train.shape[1])])
plt.show()

从图中可以看出，映射到 30 维左右就能保留大部分信息。

1
2
3

pca = PCA(0.95)
pca.fit(x_train)
pca.n_components_

Output：28

x_train_reduction = pca.transform(x_train)
x_test_reduction = pca.transform(x_test)
knn_clf = KNeighborsClassifier()
knn_clf.fit(x_train_reduction, y_train)
knn_clf.score(x_test_reduction, y_test)

Output：0.9833333333333333

PCA的特点

作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。
PCA算法的主要优点有：

　　　　1）仅仅需要以方差衡量信息量，不受数据集以外的因素影响。　

　　　　2）各主成分之间正交，可消除原始数据成分间的相互影响的因素。

　　　　3）计算方法简单，主要运算是特征值分解，易于实现。

　　　　PCA算法的主要缺点有：

　　　　1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。

　　　　2）方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

cbw

机器学习(四)——PCA主成分分析

引言

PCA的思想

sklearn中的PCA

PCA的特点