cbw

blog

0%

机器学习(八)——决策树

发表于 分类于

决策树是基于树结构进行决策的。决策树(Decision Tree）是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率。它是一种非参数学习算法，既可以解决分类问题，也可以解决回归问题。

在学习决策树前需要先对熵的概念进行了解。

信息熵

熵：用来描述事物的混乱程度，是对平均不确定性的度量。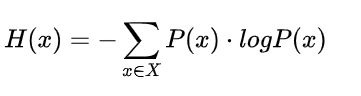

信息熵：由香农提出，。是度量样本集合纯度的最常用的指标。熵在信息论中代表随机变量不确定度的度量。一条信息大小和它的不确定性有直接关系，要搞清楚一件非常不确定的事情，或者是我们一无所知的事情，需要了解大量信息==>信息的度量就等于不确定的多少。

熵越大，数据不确定性越高，熵越低，数据的不确定性越低。假定当前样本集合D中k类样本所占比例为 pi，则信息熵的定义：

1
2
3
4
5
6
7
8
9
import numpy as np
import matplotlib.pyplot as plt

def entropy(p):
    return -p * np.log(p) - (1-p) * np.log(1-p)

x = np.linspace(0.01, 0.99, 200)
plt.plot(x, entropy(x))
plt.show()

基于信息熵的决策树

决策树的生成是一个递归过程，在决策树基本算法中有三种形式会导致递归结束并返回：
（1）当前结点包含所有的样本属于同一级别，无需划分；
（2）当前属性及为空，或是所有样本在所有属性上取值相同，无法划分；
（3）当前结点包含的样本集合为空，不能划分。
模拟信息熵进行划分：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
x = iris.data[:, 2:]
y = iris.target

def split(x, y, d, value):
    index_a = (x[:, d] <= value)
    index_b = (x[:, d] > value)
    return x[index_a], x[index_b], y[index_a], y[index_b]

from collections import Counter
from math import log 

def entropy(y):
    counter = Counter(y)
    res = 0.0
    for num in counter.values():
        p = num / len(y)
        res += -p * log(p)
        
    return res

def try_split(x, y):
    
    best_entropy = float('inf')
    best_d, best_v = -1, -1
    # 在使用的鸢尾花数据中只用了后两维，x.shape=(150, 2)
    # 首先将数据进行排序
    for d in range(x.shape[1]):
        sorted_index = np.argsort(x[:,d])
        # 经过排序后，遍历每个划分点，比较划分后的信息熵，从而选择信息增益最大的那个节点
        for i in range(1, len(x)):
            if x[sorted_index[i-1], d] != x[sorted_index[i], d]:
                v = (x[sorted_index[i-1], d] + x[sorted_index[i], d]) / 2
                x_l, x_r, y_l, y_r = split(x, y, d, v)
                e = entropy(y_l) + entropy(y_r)
                if e < best_entropy:
                    best_entropy, best_d, best_v = e, d, v
                    
    return best_entropy, best_d, best_v

best_entropy, best_d, best_v = try_split(x, y)
print('best_entropy=', best_entropy)
print('best_d=', best_d)
print('best_v2',best_v)
# best_entropy= 0.6931471805599453
# best_d= 0
# best_v2 2.45
x1_l, x1_r, y1_l, y1_r = split(x, y, best_d, best_v)
entropy(y1_l)
# 0.0
entropy(y1_r)
# 0.6931471805599453
best_entropy2, best_d2, best_v2 = try_split(x1_r, y1_r)
print('best_entropy2=', best_entropy2)
print('best_d2=', best_d2)
print('best_v2=',best_v2)
# best_entropy2= 0.4132278899361904
# best_d2= 1
# best_v2= 1.75

x2_l, x2_r, y2_l, y2_r = split(x1_r, y1_r, best_d2, best_v2)
entropy(y2_l)
# 0.30849545083110386
entropy(y2_r)
# 0.10473243910508653

根据输出结果，第一次分割节点在（d=0）第一个维度的2.45处。第二次分割节点（d2=1）在第二个维度的1.75处。
基于信息熵的划分有有两种：

基尼指数

CART（Classification and Regression Tree） 决策树使用基尼指数来选择划分属性，数据集D的纯度可以使用基尼值来度量：

1
2
3
4
5
6
7
8
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0.01, 0.99, 200)
y = -2 * x**2 + 2*x 

plt.plot(x, y)
plt.show()


接下来模拟gini指数进行划分：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
from collections import Counter
from math import log 

def split(x, y, d, value):
    index_a = (x[:, d] <= value)
    index_b = (x[:, d] > value)
    return x[index_a], x[index_b], y[index_a], y[index_b]

def gini(y):
    counter = Counter(y)
    res = 1.0
    for num in counter.values():
        p = num / len(y)
        res += -p ** 2
        
    return res

def try_split(x, y):
    
    best_g = float('inf')
    best_d, best_v = -1, -1
    for d in range(x.shape[1]):
        sorted_index = np.argsort(x[:,d])
        for i in range(1, len(x)):
            if x[sorted_index[i-1], d] != x[sorted_index[i], d]:
                v = (x[sorted_index[i-1], d] + x[sorted_index[i], d]) / 2
                x_l, x_r, y_l, y_r = split(x, y, d, v)
                g = gini(y_l) + gini(y_r)
                if g < best_g:
                    best_g, best_d, best_v = g, d, v
                    
    return best_g, best_d, best_v

best_g, best_d, best_v = try_split(x, y)
print('best_g=', best_g)
print('best_d=', best_d)
print('best_v=', best_v)
# best_g= 0.5
# best_d= 0
# best_v= 2.45

x1_l, x1_r, y1_l, y1_r = split(x, y, best_d, best_v)
gini(y1_l)
# 0.0
gini(y1_r)
# 0.5
best_g2, best_d2, best_v2 = try_split(x1_r, y1_r)
print('best_g2=', best_g2)
print('best_d2=', best_d2)
print('best_v2=', best_v2)
# best_g2= 0.2105714900645938
# best_d2= 1
# best_v2= 1.75

x2_l, x2_r, y2_l, y2_r = split(x1_r, y1_r, best_d2, best_v2)
gini(y2_l)
# 0.1680384087791495
gini(y2_r)
# 0.04253308128544431

在实际使用的过程中信息熵的计算比基尼系数稍微慢，所以 sklearn 中默认为基尼系数。对比前面的内容也能发现，大多数情况这二者并没有特别的效果优劣。

sklearn中的决策树

使用鸢尾花数据集

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
x = iris.data[:, 2:]
y = iris.target

plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.scatter(x[y==2, 0], x[y==2, 1])
plt.show()


使用基于信息熵的决策树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from sklearn.tree import DecisionTreeClassifier

dt_clf = DecisionTreeClassifier(max_depth=2, criterion='entropy')
dt_clf.fit(x, y)

def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0])*100)).reshape(1, -1),
                         np.linspace(axis[2], axis[3], int((axis[3] - axis[2])*100)).reshape(1, -1),)
    x_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(x_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])

    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.scatter(x[y==2, 0], x[y==2, 1])
plt.show()


使用基于基尼指数的决策树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
x = iris.data[:, 2:]
y = iris.target

from sklearn.tree import DecisionTreeClassifier

dt_clf = DecisionTreeClassifier(max_depth=2, criterion='gini')
dt_clf.fit(x, y)

def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0])*100)).reshape(1, -1),
                         np.linspace(axis[2], axis[3], int((axis[3] - axis[2])*100)).reshape(1, -1),)
    x_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(x_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])

    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.scatter(x[y==2, 0], x[y==2, 1])
plt.show()

决策树解决回归问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

boston = datasets.load_boston()
x = boston.data
y = boston.target

from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=666)

from sklearn.tree import DecisionTreeRegressor

dt_reg = DecisionTreeRegressor()
dt_reg.fit(x_train, y_train)
dt_reg.score(x_test, y_test)
# 0.6074066452266129
dt_reg.score(x_train, y_train)
# 1.0

训练分数很高，测试分数比较低，明显是发生了过拟合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
param_grid = [
    {
        'max_depth':[i for i in range(1, 10)],
        'min_samples_leaf':[i for i in range(1, 20)],
        'min_samples_split':[i for i in range(10, 30)],
    }
]

from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeRegressor

dt_reg3 = DecisionTreeRegressor()
grid_search = GridSearchCV(dt_reg3, param_grid)
grid_search.fit(x_train, y_train)

grid_search.best_params_
# {'max_depth': 9, 'min_samples_leaf': 1, 'min_samples_split': 23}
dt_reg4 = DecisionTreeRegressor(max_depth=9, min_samples_leaf=1, min_samples_split=23)
dt_reg4.fit(x_train, y_train)
dt_reg4.score(x_train, y_train)
# 0.9095986627498869
dt_reg4.score(x_test, y_test)
# 0.7748706184452597

透过学习曲线了解模型过拟合情况：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from sklearn.metrics import mean_squared_error

def plot_learning_curve(algo, x_train, x_test, y_train, y_test):

    train_score = []
    test_score = []
    for i in range(1, len(x_train)+1):
        algo.fit(x_train[:i], y_train[:i])

        y_train_predict = algo.predict(x_train[:i])
        train_score.append(mean_squared_error(y_train[:i], y_train_predict))

        y_test_predict = algo.predict(x_test)
        test_score.append(mean_squared_error(y_test, y_test_predict))

    plt.plot([i for i in range(1, len(x_train)+1)], np.sqrt(train_score), label='train')
    plt.plot([i for i in range(1, len(x_train)+1)], np.sqrt(test_score), label='test')
    plt.legend()
    # plt.axis([0, len(x_train)+1, 0, 4])
    plt.show()

plot_learning_curve(DecisionTreeRegressor(max_depth=9, min_samples_leaf=1, min_samples_split=23), x_train, x_test, y_train, y_test)


绘制模型复杂度曲线：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score

maxSampleLeaf = 506
train_scores = []
test_scores = []
for i in range(1, maxSampleLeaf+1):
    dt_reg = DecisionTreeRegressor(min_samples_leaf=i)
    dt_reg.fit(x_train, y_train)
    y_train_predict = dt_reg.predict(x_train)
    train_scores.append(r2_score(y_train, y_train_predict))
    test_scores.append(dt_reg.score(x_test, y_test))
    
plt.plot([i for i in range(1, maxSampleLeaf+1)], train_scores, label="train")
plt.plot([i for i in range(1, maxSampleLeaf+1)], test_scores, label="test")
plt.xlim(506, 1)
plt.legend()
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
maxSampleLeaf = 100
train_scores = []
test_scores = []
for i in range(1, maxSampleLeaf+1):
    dt_reg = DecisionTreeRegressor(min_samples_leaf=i)
    dt_reg.fit(x_train, y_train)
    y_train_predict = dt_reg.predict(x_train)
    train_scores.append(r2_score(y_train, y_train_predict))
    test_scores.append(dt_reg.score(x_test, y_test))
    
plt.plot([i for i in range(1, maxSampleLeaf+1)], train_scores, label="train")
plt.plot([i for i in range(1, maxSampleLeaf+1)], test_scores, label="test")
plt.xlim(maxSampleLeaf, 1)
plt.legend()
plt.show()

决策树的局限性

局限性1：横平竖直的直线划分，并不是能使用斜线。因此并不是最好的划分方式。

局限性2：对个别数据敏感。这也是非参数学习的一个共性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
x = iris.data[:, 2:]
y = iris.target

from sklearn.tree import DecisionTreeClassifier

dt_clf = DecisionTreeClassifier(max_depth=2, criterion='entropy')
dt_clf.fit(x, y)

def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0])*100)).reshape(1, -1),
                         np.linspace(axis[2], axis[3], int((axis[3] - axis[2])*100)).reshape(1, -1),)
    x_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(x_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])

    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.scatter(x[y==2, 0], x[y==2, 1])
plt.show()

1
2
3
4
5
6
7
8
9
10
11
x_new = np.delete(x, 138, axis=0)
y_new = np.delete(y, 138)

dt_clf2 = DecisionTreeClassifier(max_depth=2, criterion='entropy')
dt_clf2.fit(x_new, y_new)

plot_decision_boundary(dt_clf2, axis=[0.5, 7.5, 0, 3])
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.scatter(x[y==2, 0], x[y==2, 1])
plt.show()


删除了x中的一个数据，最终的到模型就大不相同，这是因为对于非参数学习来说对于个别数据十分敏感，而且非常依赖于调参才能得到一个比较好的模型。因此一般不会单独使用决策树建立模型。

-------------本文结束感谢您的阅读-------------