k均值聚类算法（k-means clustering algorithm）是一种迭代求解的聚类分析算法，其步骤是随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。

Kmeans介绍

算法接受参数k，然后将事先输入的n个数据划分为k个聚类以便使得所获得的聚类满足同一聚类中的对象相似度高，而不同聚类中的相似度低。以空间中k个中心进行聚类，对最靠近他们的对象归类，通过迭代的方法，逐次更新聚类中心的值，直至得到最好的聚类结果。

算法描述：
（1）适当选择c个类的初始中心；
（2）在k次迭代中，对任意一个样本，求其到c各中心的距离，将该样本归到距离更短的中心所在的类；
（3）利用均值等方法更新该类的中心值；
（4）对于所有的c个聚类中心，如果利用（2）（3）的迭代法更新后，值保持不变，则迭代结束，否则继续迭代。

相似度的度量

Kmeans的计算过程

现在有4组数据，每组数据有2个维度，对其进行聚类分为2类，将其可视化一下。 A=(1,1),B=(2,1),C=(4,3),D=(5,4)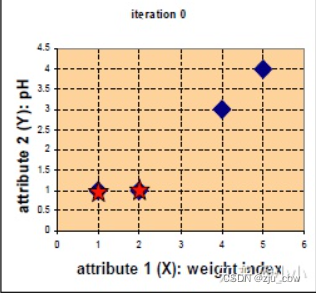

假设选取两个星的位置为初始中心 c1=(1,1),c2=(2,1) ，计算每个点到初始中心的距离，使用欧式距离得到4个点分别距离两个初始中心的距离，归于最近的类：

通过比较，将其进行归类。并使用平均法更新中心位置。

由于归于group1的只有一个点，一次更新后的中心位置 c1=(1,1)，而 c2=(11/3, 8/3)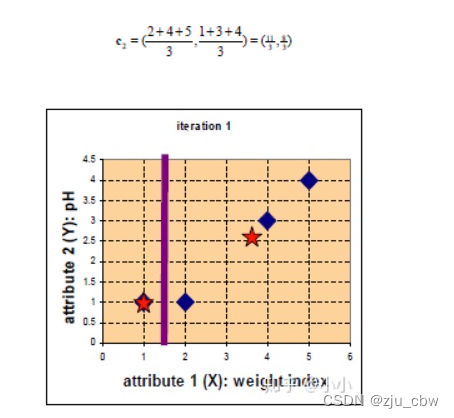

再次计算每个点与更新后的位置中心的距离

继续迭代下去，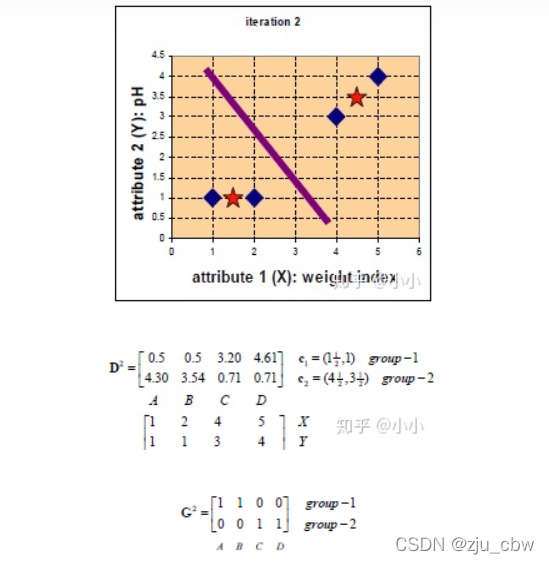

此时，与上一次的类别标记无变化，即可停止。

Kmeans的编程实现

import numpy as np

def kmeans(X, k, maxIt):
    
    numPoints, numDim = X.shape
    # 给数据标签留个位置
    dataSet = np.zeros((numPoints, numDim + 1))
    dataSet[:, :-1] = X
    
    # 随机初始化位置中心
    centroids = dataSet[np.random.randint(numPoints, size = k), :]
    centroids = dataSet[0:2, :]
    # 随机给初始位置中心赋予类别标记
    centroids[:, -1] = range(1, k +1)
    
    iterations = 0
    oldCentroids = None
    
    # Run the main k-means algorithm
    while not shouldStop(oldCentroids, centroids, iterations, maxIt):
        print("iteration: \n", iterations)
        print("dataSet: \n", dataSet)
        print("centroids: \n", centroids)
        # Save old centroids for convergence test. Book keeping.
        oldCentroids = np.copy(centroids)
        iterations += 1
        
        # Assign labels to each datapoint based on centroids
        updateLabels(dataSet, centroids)
        
        # Assign centroids based on datapoint labels
        centroids = getCentroids(dataSet, k)
        
    # We can get the labels too by calling getLabels(dataSet, centroids)
    return dataSet

def shouldStop(oldCentroids, centroids, iterations, maxIt):
    if iterations > maxIt:
        return True
    return np.array_equal(oldCentroids, centroids)  

def updateLabels(dataSet, centroids):
    # For each element in the dataset, chose the closest centroid. 
    # Make that centroid the element's label.
    numPoints, numDim = dataSet.shape
    for i in range(0, numPoints):
        dataSet[i, -1] = getLabelFromClosestCentroid(dataSet[i, :-1], centroids)
        
def getLabelFromClosestCentroid(dataSetRow, centroids):
    label = centroids[0, -1];
    minDist = np.linalg.norm(dataSetRow - centroids[0, :-1])
    for i in range(1 , centroids.shape[0]):
        dist = np.linalg.norm(dataSetRow - centroids[i, :-1])
        if dist < minDist:
            minDist = dist
            label = centroids[i, -1]
    print("minDist:", minDist)
    return label

def getCentroids(dataSet, k):
    # Each centroid is the geometric mean of the points that
    # have that centroid's label. Important: If a centroid is empty (no points have
    # that centroid's label) you should randomly re-initialize it.
    result = np.zeros((k, dataSet.shape[1]))
    for i in range(1, k + 1):
        oneCluster = dataSet[dataSet[:, -1] == i, :-1]
        result[i - 1, :-1] = np.mean(oneCluster, axis = 0)
        result[i - 1, -1] = i
    
    return result

x1 = np.array([1, 1])
x2 = np.array([2, 1])
x3 = np.array([4, 3])
x4 = np.array([5, 4])
testX = np.vstack((x1, x2, x3, x4))

result = kmeans(testX, 2, 10)
print("final result:")
print(result)
# final result:
# [[1. 1. 1.]
#  [2. 1. 1.]
#  [4. 3. 2.]
#  [5. 4. 2.]]

sklearn包的Kmeans聚类

from sklearn.cluster import KMeans
KMeans(n_clusters=8,init='k-means++',n_init=10,max_iter=300,tol=0.0001, 
       verbose=0,random_state=None,
       copy_x=True,algorithm='auto')

参数

n_clusters：
整形，默认=8 【生成的聚类数，即产生的质心（centroids）数

init：
有三个可选值：'k-means++'， 'random'，或者传递一个ndarray向量。
此参数指定初始化方法，默认值为 'k-means++'。
（１）'k-means++' 用一种特殊的方法选定初始质心从而能加速迭代过程的收敛
（２）'random' 随机从训练数据中选取初始质心。
（３）如果传递的是一个ndarray，则应该形如 (n_clusters, n_features) 并给出初始质心

n_init：
整形，默认=10用不同的质心初始化值运行算法的次数，最终解是在inertia意义下选出的最优结果

max_iter：
整形，默认=300执行一次k-means算法所进行的最大迭代数

tol：
float形，默认值= 1e-4　与inertia结合来确定收敛条件

precompute_distances：
三个可选值，'auto'，True 或者 False。预计算距离，计算速度更快但占用更多内存。
（１）'auto'：如果 样本数乘以聚类数大于 12million 的话则不预计算距离
（２）True：总是预先计算距离
（３）False：永远不预先计算距离
自版本0.23起已弃用： 'precompute_distances'在版本0.22中已弃用，并将在0.25中删除。没有作用

verbose：
int 默认为0，Verbosity mode

random_state：
整形或 numpy.RandomState 类型，可选用于初始化质心的生成器（generator）
如果值为一个整数，则确定一个seed。此参数默认值为numpy的随机数生成器

copy_x：
布尔型，默认值=True
当我们precomputing distances时，将数据中心化会得到更准确的结果
如果把此参数值设为True，则原始数据不会被改变
如果是False，则会直接在原始数据上做修改并在函数返回值时将其还原
但是在计算过程中由于有对数据均值的加减运算，所以数据返回后，原始数据和计算前可能会有细小差别

n_jobs：
整形数。　指定计算所用的进程数。内部原理是同时进行n_init指定次数的计算。
（１）若值为 -1，则用所有的CPU进行运算
（2）若值为1，则不进行并行运算，这样的话方便调试
（3）若值小于-1，则用到的CPU数为(n_cpus + 1 + n_jobs)
         如果 n_jobs值为-2，则用到的CPU数为总CPU数减1
  从0.23版n_jobs开始不推荐使用：从0.23版开始不推荐使用，并将在0.25版中删除。 
  
algorithm：
三种可选“auto”, “full”, “elkan”, default=”auto”
 使用K均值算法。经典的EM风格算法是“full”的
 通过使用三角形不等式，“ elkan”算法对于定义良好的聚类的数据更有效
 但是，由于分配了额外的形状数组（n_samples，n_clusters），因此需要更多的内存。
目前，“ auto”（保持向后兼容性）选择“ elkan”
在版本0.18中更改：添加了Elkan算法

实例
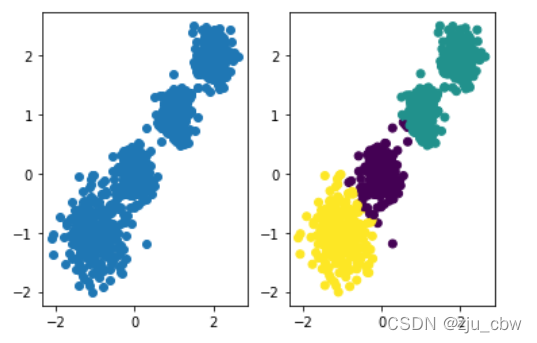
首先我们随机创建一些二维数据作为训练集，观察在不同的k值下聚类算法的区别

import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# X为样本特征，Y为样本簇类别， 共1000个样本，
# 每个样本4个特征，共4个簇，簇中心在[-1,-1], [0,0],[1,1],[2,2]， 簇方差分别为[0.4, 0.2, 0.2，0.2]
X, y = make_blobs(n_samples=1000, n_features=2,centers=[[-1,-1], [0,0], [1,1], [2,2]],
cluster_std=[0.4, 0.2, 0.2, 0.2],random_state =9)
y_pred = KMeans(n_clusters=2, random_state=9)
y_pred = y_pred.fit_predict(X)
plt.figure()
plt.subplot(1,2,1)
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.subplot(1,2,2)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

利用KMeans函数新建一个聚类算法，这里设置为2分类

1	y_pred = KMeans(n_clusters=2, random_state=9)

然后进行分类

y_pred = y_pred.fit_predict(X)
 新建对象后，常用的方法包括fit、predict、cluster_centers_和labels。
 fit（X）函数对数据X进行聚类，
 使用predict方法进行新数据类别的预测，
 使用cluster_centers_获取聚类中心，
 使用labels_获取训练数据所属的类别，
 inertia_获取每个点到聚类中心的距离和

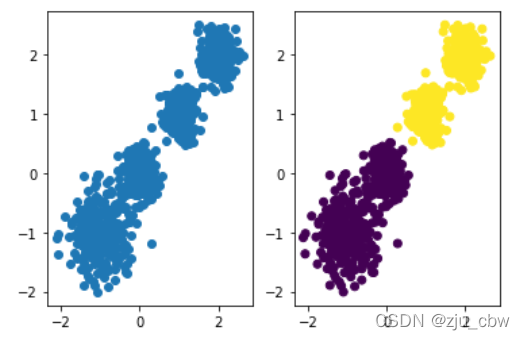
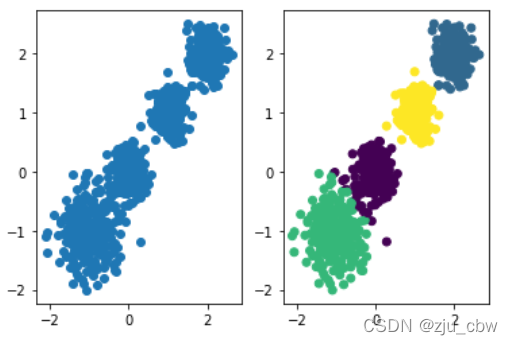
当然3分类，4分类我们只需要修改一下KMeans函数中的n_clusters参数即可

1 2	y_pred = KMeans(n_clusters=3, random_state=9) y_pred = KMeans(n_clusters=4, random_state=9)

cbw

机器学习(九)——Kmeans聚类

Kmeans介绍

相似度的度量

Kmeans的计算过程

Kmeans的编程实现