cbw

blog

0%

深度学习(七)——Batch Normalization+Pytorch实现

发表于 分类于

简介

Batch Normalization是如今深度学习常见的方法，来加速深层网络训练的收敛，并且有正则化的作用，甚至可以不使用Dropout或者减小神经元被drop的概率。

原理

深度神经网络训练的问题

深度神经网络模型的训练为什么困难、收敛慢？这个问题的解决在之前的工作中，有从尝试新的激活函数角度，如 ReLU、Maxout、PReLU等；有从权值初始化方法角度，如Xavier初始化、Kaiming初始化等，但收益相对都不是很高。

这个问题的存在使得在设置 learning rate、初始化方法还有激活函数上得要很慎重，而这个问题的实质是因为在训练过程中，随着前一层参数的改变，哪怕很小的改变，也会因为网络加深而被放大，而这种改变使得每一层输入的分布发生改变，从而每一层需要持续地适应这种改变，这种现象在论文中被称为 Internal covariate shift （ICS，内部协变量偏移）。

从另外一个角度看，把网络的中间层看作是 sub-network 以及采用 sigmoid 激活函数 z = g ( W u + b )，其中 u 是该层的输入，而 W 和 b 是学习的参数。随着 ∣ x ∣ 增大，g ′ ( x ) 趋向于0，这也就意味着会发生我们熟知的梯度消失（本质是落入饱和区），后来 ReLU 和 一些初始化方法是较好的缓解了这个问题。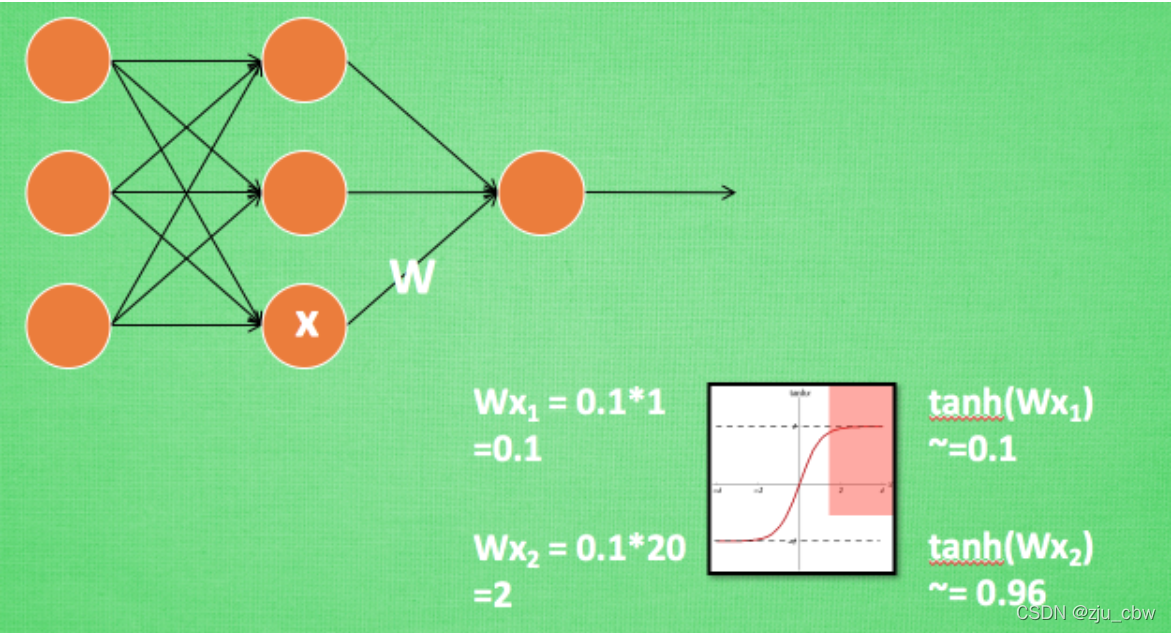

换一个思路想，造成这个问题比较直观的原因是因为 ∣ x ∣ 的增大，即输入分布的变化，以及上面提到的 ICS 现象也是因为每一层的输入分布发生改变，那么很自然的想法就是，如果能确保输入的分布稳定，那么就不容易陷入饱和区域，从而梯度消失的问题也就得到很好的缓和，训练收敛的速度也随之提升了，问题就迎刃而解了。

看着好像蛮简单的，但还是有随之而来的问题：

  • 确保输入的分布稳定，即 Normalization ，该怎么做？
  • Normalization 能使得输入不落入饱和区域，反过来就是限制输入落入激活函数的线性区域，那这样网络不就失去了非线性的表达能力了吗，这该怎么弥补？

上面的两个也就是 Batch Normalization 这篇论文工作的核心。

解决方法

白化（whitening） 作为一个很重要的数据预处理方法，它能使得模型训练收敛的更快，而白化一般包含两个目的：

  • 去除特征之间的相关性（特征独立）；
  • 使得所有特征具有相同的均值和方差（同分布）

白化可以使得模型的输入标准化为均值为0，方差为1，那可以考虑将白化拓展到每一层的输入，就能使得每一层的分布趋于稳定。然而，标准的白化操作代价昂贵，特别是我们还希望白化操作是可微的，保证白化操作可以通过反向传播来更新梯度，即：

于是就有了本篇论文的工作，Batch Normalization（BN），即对白化做了简化，将其作用到每一层的输入，使得输入分布稳定。
第一个简化是只对每一个特征维度做 Normalization，并没有考虑特征之间去相关，论文中也提到了，“such normalization speeds up convergence, even when the features are not decorrelated.”，即：

第二个简化是不通过整个数据集来统计 E[x^(k)^] 和 Var[x^(k)^] 和而是通过一个 mini-batch 内的激活值来估计均值和方差 ，得到：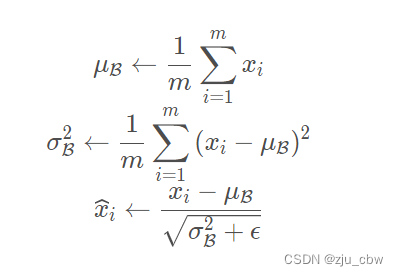

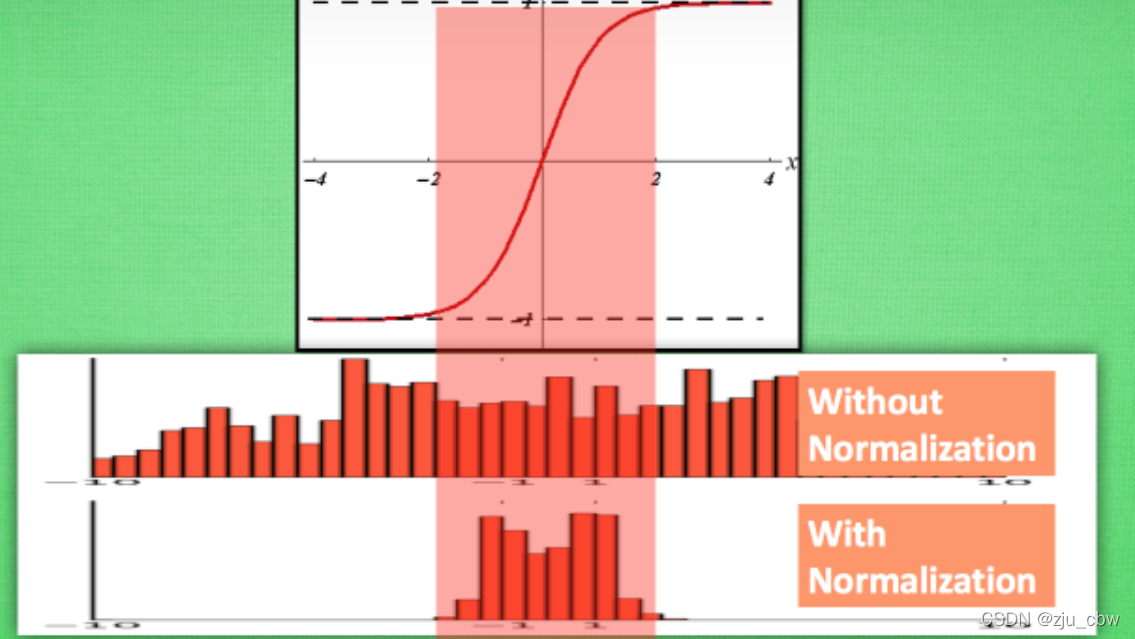
而这样的 Normalization 是存在问题的，如论文中提到 “*simply normalizing each input of a layer may change what the layer can represent.*”，即简单地做 Normalization 会减低了网络的非线性的表达能力，比如采用 sigmoid 激活函数，normalization 会限制激活值落入到线性区域（近似线性），而这片区域是近似 [-2, 2] 这个区间，而在标准正态分布中，落入 [-2, 2] 的概率是95%。
这也就前面提到问题，作者采用的方式是 “make sure that the transformation inserted in the network can represent the identity transform”，为了实现这种可以恒等变换，引入了两个可学习的参数 γ^(k)^ 和 β^(k)^，使得：

而在最极端的情况下，学习的两个参数分别为

，则可以恢复到原先的激活值，即恢复了网络的表达能力（restore the representation power of the network）。
Batch Normalization 大致的算法过程如下：

BN 采用 mini-batch 来估计均值和方差，这在训练的时候是可行的，但在 inference 或 online inference 时，是单实例的，不存在 mini-batch，所以就无法获得BN计算所需的均值和方差，这就需要利用训练阶段的Batch统计值，估计一个总体的均值和方差，从而实现 inference 阶段的 normalization：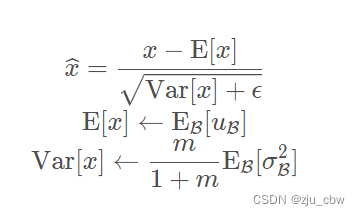

值得注意的是，在PyTorch代码实现的时候，会去采用指数滑动平均（Exponential Moving Average）来实现总体的估计，见PyTorch文档描述：

更高的学习率

在论文摘要部分提到了，“Batch Normalization allows us to use much higher learning rates and be less careful about initialization.”，在还没看正文时，就有疑问，为什么 BN 可以使得采用更大的学习率？作者专门在一小节中对其进行了解释。

通常在训练深层网络，不会使用太大的学习率，因为它易导致梯度爆炸、梯度消失或者陷入到 poor local minima。而前面也提到，BN 能够一定程度上避免输入落入到激活函数的饱和区域，缓解了梯度消失的问题；另外因为每层输入都有 normalization 的存在，缓解了 ICS 的存在，使得每层的输入分布稳定，参数的变化（反向传播的梯度）也趋于稳定（不会因为随着层数加深，参数变化被放大），较好地缓解了梯度爆炸。

论文中称 “Batch Normalization also makes training more resilient to parameter scale” ，并对这种参数更新（梯度）的稳定做了一个分析。因为通常，较大的学习率会使得参数的规模增大（increase the scale of layer parameters），假设增大了 a 倍，但因为 BN 的存在，反向传播并不会受到参数增大的影响，从而导致的梯度爆炸：

第三个式子还能看到，更大的参数返回会导致更小的梯度，从而上面的结论也得到了验证：BN 的存在，使得参数变化趋于稳定，故能使用更大的学习率。

正则化

在论文的摘要中提到因为 BN 的存在，使得 Dropout 可以被移除或者减小神经元被 drop 的概率，换句话说，BN 具备了 dropout 提升模型泛化能力（缓解过拟合）的功能，主要是因为通过 batch 内的激活值估计均值和方差，不是根据单一 sample 的值做模型优化，这可以变相地看成是某一种约束。

这边有三点需要注意的是：

  • 论文中讨论将BN放在激活函数前好还是后好，“*but since u is likely the output of another nonlinearity, the shape of its distribution is likely to change during training, and constraining its first and second moments would not eliminate the covariate shift.*”，不是很明白，而 [1] 中提到 “不少研究表明将BN放在激活函数之后效果更好。” ，但并没有给出参考文献，这里还需后面验证。
  • 对于卷积层，在估计均值和方差时考虑的神经元激活值集合并不是标量特征，而是一个 feature map 内的特征值，“we jointly normalize all the activations in a mini-batch over all locations. In Alg. 1, we let B be the set of all values in a feature map across both the elements of a mini-batch and spatial locations”
  • 在 Normalization 前的线性变换 W u + b ，通常会省略掉偏置项 b ，因为它的作用会被随后BN的均值给抵消掉（它的作用会被 β 代替）。

实验

作者通过一个很简单的实验来验证BN是否能较好的缓解ICS问题。在MNIST数据集上，一个简单的三层的神经网络，在每一层之前加入BN，观察收敛速度和每层的输入分布变化，结果如下图：

另外一个实验就是在 ImageNet Classification 任务上，实验的模型结构在 Inception-v1 上做的改进是参考 VGG 中小尺寸的卷积核的思想，将 5×5 的卷积核替换为 两层 3 × 3 的卷积核，并且加宽了网络和引入了BN，另外值得注意的是，在Inception-v2的网络结构设计中，用 stride=2 代替了 Inception-v1 中 max pool 做 feature map 的尺寸缩减。
为了进一步加速 BN networks 训练收敛的速度，作者进一步改进了网络和训练的超参数：

  • Increase learning rate：在上面也提到了可以使用更大的学习率，那么增大学习率来加快模型训练；
  • Remove dropout：前面同样提到 BN 能一定程度缓解过拟合，那就将 dropout 移除来提速；
  • Reduce the L 2 weight regularization：减少 L2 正则项的权值；
  • Accelerate the learning rate decay：因为 BN 加快了模型的训练，所以相应的学习率的衰减也得加快，这里采用了指数衰减；
  • Remove Local Response Normalization：这里是移除了 LRN，其实在之前的一些工作中就不用它了；
  • Shuffle training examples more thoroughly
  • Reduce the photometric distortions
    另外，作者还做了一些调整，设置了几个模型：
  • BN-Baseline：即相较于 Inception-v1 引入了 BN；
  • BN-x5：将学习率增大了5倍，为0.0075
  • BN-x30：将学习率增大了30倍，为0.045
  • BN-x5-Sigmoid：和 BN-x5 类似，但激活函数换成了Sigmoid。
    下面是实验的结果，可以看到仅采用 BN 的Baselin 其收敛速度是快于 Inception v1，另外 BN-x5 更是快了14倍（达到Inception 的准确率），而虽 BN-x30 较之 BN-x5 会慢一些，但其准确率是最高的。有意思的是，论文中还玩了一个小小的文字游戏：we apply Batch Normalization to the bestperforming ImageNet classification network, and show that we can match its performance using only 7% of the training steps, and can further exceed its accuracy by a substantial margin. ，其实这里 7% 是由 BN-x5 实现的，而 BN-x30 是在准确率上做了提升。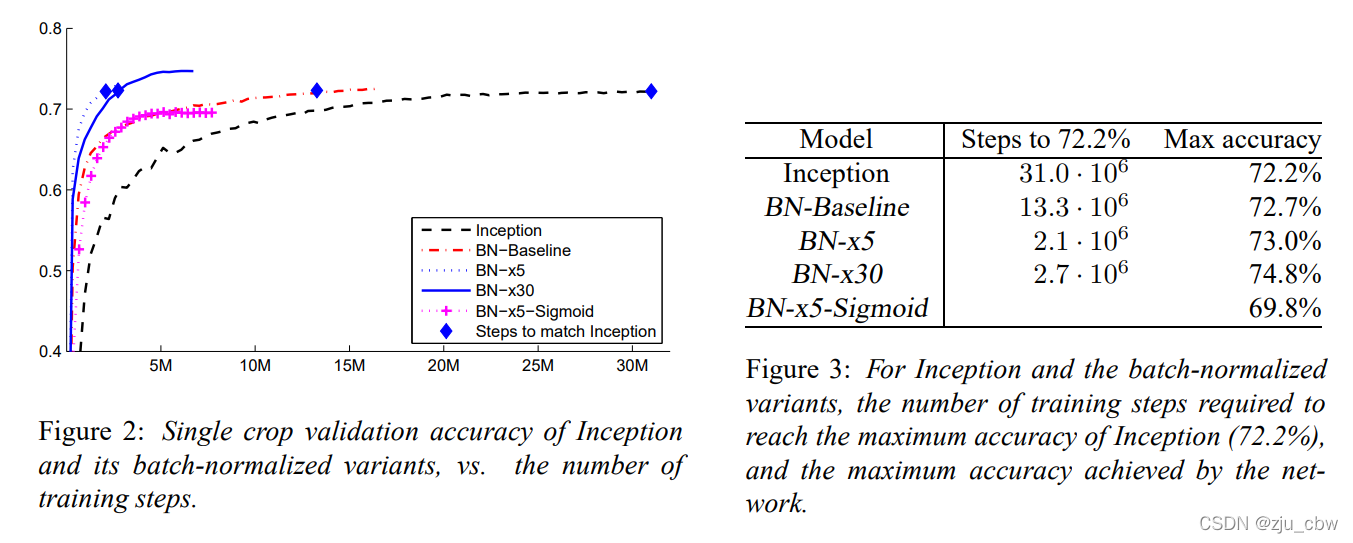

Pytorch实现

下面将Batch Normalization加入到GoogleNet中，并将5x5的卷积核用2个2x2的卷积核代替。
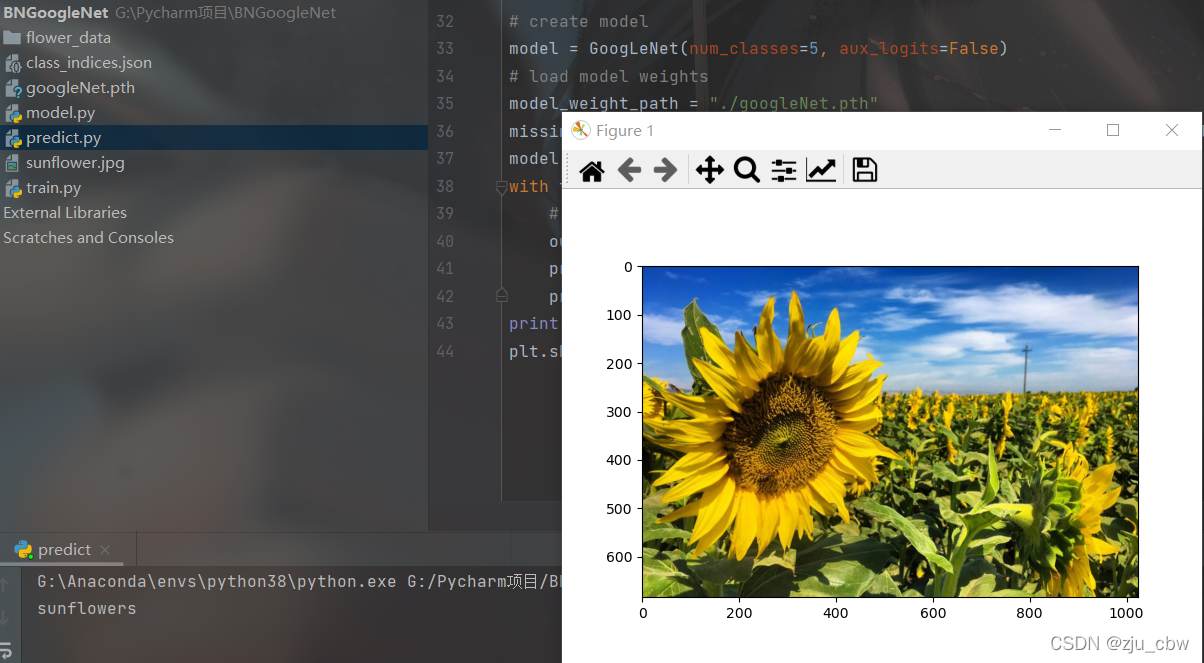
从http://download.tensorflow.org/example_images/flower_photos.tgz下载数据集
执行下面代码，将数据集划分为训练集与验证集。
split_data.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import os
from shutil import copy
import random


def mkfile(file):
    if not os.path.exists(file):
        os.makedirs(file)


file = 'flower_data/flower_photos'
flower_class = [cla for cla in os.listdir(file) if ".txt" not in cla]
mkfile('flower_data/train')
for cla in flower_class:
    mkfile('flower_data/train/'+cla)

mkfile('flower_data/val')
for cla in flower_class:
    mkfile('flower_data/val/'+cla)

split_rate = 0.1
for cla in flower_class:
    cla_path = file + '/' + cla + '/'
    images = os.listdir(cla_path)
    num = len(images)
    eval_index = random.sample(images, k=int(num*split_rate))
    for index, image in enumerate(images):
        if image in eval_index:
            image_path = cla_path + image
            new_path = 'flower_data/val/' + cla
            copy(image_path, new_path)
        else:
            image_path = cla_path + image
            new_path = 'flower_data/train/' + cla
            copy(image_path, new_path)
        print("\r[{}] processing [{}/{}]".format(cla, index+1, num), end="")  # processing bar
    print()

print("processing done!")

model.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
import torch.nn as nn
import torch
import torch.nn.functional as F


class GoogLeNet(nn.Module):
    def __init__(self, num_classes=1000, aux_logits=True, init_weights=False):
        super(GoogLeNet, self).__init__()
        self.aux_logits = aux_logits

        self.conv1 = BasicConv2d(3, 64, kernel_size=7, stride=2, padding=3)
        self.maxpool1 = nn.MaxPool2d(3, stride=2, ceil_mode=True)

        self.conv2 = BasicConv2d(64, 64, kernel_size=1)
        self.conv3 = BasicConv2d(64, 192, kernel_size=3, padding=1)
        self.maxpool2 = nn.MaxPool2d(3, stride=2, ceil_mode=True)

        self.inception3a = Inception(192, 64, 96, 128, 16, 32, 32)
        self.inception3b = Inception(256, 128, 128, 192, 32, 96, 64)
        self.maxpool3 = nn.MaxPool2d(3, stride=2, ceil_mode=True)

        self.inception4a = Inception(480, 192, 96, 208, 16, 48, 64)
        self.inception4b = Inception(512, 160, 112, 224, 24, 64, 64)
        self.inception4c = Inception(512, 128, 128, 256, 24, 64, 64)
        self.inception4d = Inception(512, 112, 144, 288, 32, 64, 64)
        self.inception4e = Inception(528, 256, 160, 320, 32, 128, 128)
        self.maxpool4 = nn.MaxPool2d(3, stride=2, ceil_mode=True)

        self.inception5a = Inception(832, 256, 160, 320, 32, 128, 128)
        self.inception5b = Inception(832, 384, 192, 384, 48, 128, 128)

        if self.aux_logits:
            self.aux1 = InceptionAux(512, num_classes)
            self.aux2 = InceptionAux(528, num_classes)

        self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
        self.dropout = nn.Dropout(0.4)
        self.fc = nn.Linear(1024, num_classes)
        if init_weights:
            self._initialize_weights()

    def forward(self, x):
        # N x 3 x 224 x 224
        x = self.conv1(x)
        # N x 64 x 112 x 112
        x = self.maxpool1(x)
        # N x 64 x 56 x 56
        x = self.conv2(x)
        # N x 64 x 56 x 56
        x = self.conv3(x)
        # N x 192 x 56 x 56
        x = self.maxpool2(x)

        # N x 192 x 28 x 28
        x = self.inception3a(x)
        # N x 256 x 28 x 28
        x = self.inception3b(x)
        # N x 480 x 28 x 28
        x = self.maxpool3(x)
        # N x 480 x 14 x 14
        x = self.inception4a(x)
        # N x 512 x 14 x 14
        if self.training and self.aux_logits:    # eval model lose this layer
            aux1 = self.aux1(x)

        x = self.inception4b(x)
        # N x 512 x 14 x 14
        x = self.inception4c(x)
        # N x 512 x 14 x 14
        x = self.inception4d(x)
        # N x 528 x 14 x 14
        if self.training and self.aux_logits:    # eval model lose this layer
            aux2 = self.aux2(x)

        x = self.inception4e(x)
        # N x 832 x 14 x 14
        x = self.maxpool4(x)
        # N x 832 x 7 x 7
        x = self.inception5a(x)
        # N x 832 x 7 x 7
        x = self.inception5b(x)
        # N x 1024 x 7 x 7

        x = self.avgpool(x)
        # N x 1024 x 1 x 1
        x = torch.flatten(x, 1)
        # N x 1024
        x = self.dropout(x)
        x = self.fc(x)
        # N x 1000 (num_classes)
        if self.training and self.aux_logits:   # eval model lose this layer
            return x, aux2, aux1
        return x

    def _initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
                if m.bias is not None:
                    nn.init.constant_(m.bias, 0)
            elif isinstance(m, nn.Linear):
                nn.init.normal_(m.weight, 0, 0.01)
                nn.init.constant_(m.bias, 0)

#inception结构
class Inception(nn.Module):
    def __init__(self, in_channels, ch1x1, ch3x3red, ch3x3, ch5x5red, ch5x5, pool_proj):
        super(Inception, self).__init__()

        self.branch1 = BasicConv2d(in_channels, ch1x1, kernel_size=1)

        self.branch2 = nn.Sequential(
            BasicConv2d(in_channels, ch3x3red, kernel_size=1),
            BasicConv2d(ch3x3red, ch3x3, kernel_size=3, padding=1)   # 保证输出大小等于输入大小
        )

        self.branch3 = nn.Sequential(
            BasicConv2d(in_channels, ch5x5red, kernel_size=1),
            BasicConv2d(ch5x5red, ch5x5, kernel_size=3, padding=1),
            BasicConv2d(ch5x5, ch5x5, kernel_size=3, padding=1)     # 保证输出大小等于输入大小
        )

        self.branch4 = nn.Sequential(
            nn.MaxPool2d(kernel_size=3, stride=1, padding=1),
            BasicConv2d(in_channels, pool_proj, kernel_size=1)
        )

    def forward(self, x):
        branch1 = self.branch1(x)
        branch2 = self.branch2(x)
        branch3 = self.branch3(x)
        branch4 = self.branch4(x)

        outputs = [branch1, branch2, branch3, branch4]
        return torch.cat(outputs, 1)

#辅助分类器
class InceptionAux(nn.Module):
    def __init__(self, in_channels, num_classes):
        super(InceptionAux, self).__init__()
        self.averagePool = nn.AvgPool2d(kernel_size=5, stride=3)
        self.conv = BasicConv2d(in_channels, 128, kernel_size=1)  # output[batch, 128, 4, 4]

        self.fc1 = nn.Linear(2048, 1024)
        self.fc2 = nn.Linear(1024, num_classes)

    def forward(self, x):
        # aux1: N x 512 x 14 x 14, aux2: N x 528 x 14 x 14
        x = self.averagePool(x)
        # aux1: N x 512 x 4 x 4, aux2: N x 528 x 4 x 4
        x = self.conv(x)
        # N x 128 x 4 x 4
        x = torch.flatten(x, 1)
        x = F.dropout(x, 0.5, training=self.training)
        # N x 2048
        x = F.relu(self.fc1(x), inplace=True)
        x = F.dropout(x, 0.5, training=self.training)
        # N x 1024
        x = self.fc2(x)
        # N x num_classes
        return x


class BasicConv2d(nn.Module):
    def __init__(self, in_channels, out_channels, **kwargs):
        super(BasicConv2d, self).__init__()
        self.conv = nn.Conv2d(in_channels, out_channels, **kwargs)
        self.bn = nn.BatchNorm2d(out_channels)
        self.relu = nn.ReLU(inplace=True)

    def forward(self, x):
        x = self.conv(x)
        x = self.bn(x)
        x = self.relu(x)
        return x

train.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
import torch
import torch.nn as nn
from torchvision import transforms, datasets
import torchvision
import json
import matplotlib.pyplot as plt
import os
import torch.optim as optim
from model import GoogLeNet

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(device)

data_transform = {
    "train": transforms.Compose([transforms.RandomResizedCrop(224),
                                 transforms.RandomHorizontalFlip(),
                                 transforms.ToTensor(),
                                 transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))]),
    "val": transforms.Compose([transforms.Resize((224, 224)),
                               transforms.ToTensor(),
                               transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])}

#data_root = os.path.abspath(os.path.join(os.getcwd(), "../.."))  # get data root path
data_root = os.getcwd()
image_path = data_root + "/flower_data/"  # flower data set path

train_dataset = datasets.ImageFolder(root=image_path + "train",
                                     transform=data_transform["train"])
train_num = len(train_dataset)

# {'daisy':0, 'dandelion':1, 'roses':2, 'sunflower':3, 'tulips':4}
flower_list = train_dataset.class_to_idx
cla_dict = dict((val, key) for key, val in flower_list.items())
# write dict into json file
json_str = json.dumps(cla_dict, indent=4)
with open('class_indices.json', 'w') as json_file:
    json_file.write(json_str)

batch_size = 32
train_loader = torch.utils.data.DataLoader(train_dataset,
                                           batch_size=batch_size, shuffle=True,
                                           num_workers=0)

validate_dataset = datasets.ImageFolder(root=image_path + "val",
                                        transform=data_transform["val"])
val_num = len(validate_dataset)
validate_loader = torch.utils.data.DataLoader(validate_dataset,
                                              batch_size=batch_size, shuffle=False,
                                              num_workers=0)

# test_data_iter = iter(validate_loader)
# test_image, test_label = test_data_iter.next()

# net = torchvision.models.googlenet(num_classes=5)
# model_dict = net.state_dict()
# pretrain_model = torch.load("googlenet.pth")
# del_list = ["aux1.fc2.weight", "aux1.fc2.bias",
#             "aux2.fc2.weight", "aux2.fc2.bias",
#             "fc.weight", "fc.bias"]
# pretrain_dict = {k: v for k, v in pretrain_model.items() if k not in del_list}
# model_dict.update(pretrain_dict)
# net.load_state_dict(model_dict)
net = GoogLeNet(num_classes=5, aux_logits=True, init_weights=True)
net.to(device)
loss_function = nn.CrossEntropyLoss()
optimizer = optim.Adam(net.parameters(), lr=0.0015)
scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=1500, gamma=0.1) # 权重衰减策略

best_acc = 0.0
save_path = './googleNet.pth'
for epoch in range(30):
    # train
    net.train()
    running_loss = 0.0
    for step, data in enumerate(train_loader, start=0):
        images, labels = data
        optimizer.zero_grad()
        logits, aux_logits2, aux_logits1 = net(images.to(device))
        loss0 = loss_function(logits, labels.to(device))
        loss1 = loss_function(aux_logits1, labels.to(device))
        loss2 = loss_function(aux_logits2, labels.to(device))
        loss = loss0 + loss1 * 0.3 + loss2 * 0.3
        loss.backward()
        optimizer.step()
        scheduler.step()

        # print statistics
        running_loss += loss.item()
        # print train process
        rate = (step + 1) / len(train_loader)
        a = "*" * int(rate * 50)
        b = "." * int((1 - rate) * 50)
        print("\rtrain loss: {:^3.0f}%[{}->{}]{:.3f}".format(int(rate * 100), a, b, loss), end="")
    print()

    # validate
    net.eval()
    acc = 0.0  # accumulate accurate number / epoch
    with torch.no_grad():
        for val_data in validate_loader:
            val_images, val_labels = val_data
            outputs = net(val_images.to(device))  # eval model only have last output layer
            predict_y = torch.max(outputs, dim=1)[1]
            acc += (predict_y == val_labels.to(device)).sum().item()
        val_accurate = acc / val_num
        if val_accurate > best_acc:
            best_acc = val_accurate
            torch.save(net.state_dict(), save_path)
        print('[epoch %d] train_loss: %.3f  test_accuracy: %.3f' %
              (epoch + 1, running_loss / step, val_accurate))

print('Finished Training')

Output:

predict.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import torch
from model import GoogLeNet
from PIL import Image
from torchvision import transforms
import matplotlib.pyplot as plt
import json
import os

os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"

data_transform = transforms.Compose(
    [transforms.Resize((224, 224)),
     transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

# load image
img = Image.open("./sunflower.jpg")
plt.imshow(img)
# [N, C, H, W]
img = data_transform(img)
# expand batch dimension
img = torch.unsqueeze(img, dim=0)

# read class_indict
try:
    json_file = open('./class_indices.json', 'r')
    class_indict = json.load(json_file)
except Exception as e:
    print(e)
    exit(-1)

# create model
model = GoogLeNet(num_classes=5, aux_logits=False)
# load model weights
model_weight_path = "./googleNet.pth"
missing_keys, unexpected_keys = model.load_state_dict(torch.load(model_weight_path), strict=False)
model.eval()
with torch.no_grad():
    # predict class
    output = torch.squeeze(model(img))
    predict = torch.softmax(output, dim=0)
    predict_cla = torch.argmax(predict).numpy()
print(class_indict[str(predict_cla)])
plt.show()

Output:

-------------本文结束感谢您的阅读-------------